This page was last updated on March 20, 2024.

Background

Simulation is an important tool for carrying out computational and statistical biology. This page provides basic guidance on how to simulate data in R.

Simulating from Distributions

R comes with built in tools that allow you to simulate from well-known probability distributions like the normal, Poisson, binomial, uniform, chi-squared, and so on (for a complete list see: help(Distributions) )

There are 4 functions for working with distributions that have the general form:

  • dxxx for the density/mass function (PDF/PMF)
  • pxxx for the cumulative distribution function (CDF)
  • qxxx for the quantile function
  • rxxx for random number generation


Normal

The rnorm function is the base function for simulating random numbers drawn from a normal distribution. For more information on working with the normal distribution see help(Normal)

rnorm(n = 5,                  # number of observations
      mean = 0,               # vector of means
      sd = 1)                 # vector of standard deviations
## [1] 0.9930842 0.6740632 0.9034885 1.7130176 1.0075470

Because rnorm is expecting a vector for each entry, this function is very flexible. For example we can sample 5 values from normal distributions with different means and different standard deviations without having to re-write the function 5 times.

rnorm(n = 5,                  # number of observations
      mean = c(1,2,3,4,5),    # vector of means
      sd = 1:5)               # vector of standard deviations
## [1]  1.720988  4.099509 -1.546716  5.468813 -1.002096

Poisson

The rpois function is the base function for simulating random numbers drawn from a Poisson distribution. For more information on working with the Poisson distribution see help(Poisson)

Note: Will only return whole numbers

rpois(n = 5,                  # number of observations
      lambda = 1)             # vector of (non-negative) rate parameters
## [1] 0 1 0 1 1

Because rpois is expecting a vector for each entry, this function is very flexible. For example we can sample 5 values from Poisson distributions with different rate parameters \(\lambda\), without having to re-write the function 5 times.

rpois(n = 5,                  # number of observations
      lambda = c(1,2,3,4,5))  # vector of (non-negative) rate parameters
## [1] 2 2 4 3 6

Binomial

The rbinom function is the base function for simulating random numbers drawn from a binomial distribution. For more information on working with the binomial distribution see help(Binomial)

rbinom(n = 5,                  # number of observations
       size = 1,               # number of trials (zero or more)
       prob = 0.5)             # probability of success on each trial.
## [1] 1 0 1 1 0

If we change the number of trials we get the number of successes across the number of trials. In this example we have simulated the number of successes in 5 replicates of 20 trials.

rbinom(n = 5,                  # number of observations
       size = 20,              # number of trials (zero or more)
       prob = 0.5)             # probability of success on each trial.
## [1]  8 14  9 10 11

Because rbinom is expecting a vector for each entry, this function is very flexible. For example we can simulate the number of successes in 5 replicates of 20 trials, with a different probability of success in each trial

rbinom(n = 5,
       size = 20,
       prob = c(0.2, 0.4, 0.6, 0.8, 1))
## [1]  2  9 14 17 20

Uniform

The runif function is the base function for simulating random numbers drawn from a uniform distribution. For more information on working with the uniform distribution see help(Uniform)

runif(n = 5,                  # number of observations
      min = 0,                # lower limit of the distribution. Must be finite.
      max = 20)               # upper limit of the distribution. Must be finite.
## [1] 17.560604 11.767825  8.488491  2.813352 10.708172

Unlike the other distributions runif is not expecting vector for the min and max arguments, so this function does not have the same amount of inherent flexibility.

Setting the Seed

When simulating random numbers, setting the random number seed with set.seed() ensures reproducibility of the sequence of random numbers.

For example, we can sample 5 random numbers from a normal distribution with rnorm().

rnorm(5)
## [1]  0.5405435  0.6899546  0.3066125 -0.1786901  0.2000035

If we do this a second time the sequence of numbers will always be different.

rnorm(5)
## [1] -0.91397987 -0.89726293  0.05836574  1.40688290 -0.48700109

But if we want to be sure we can get the same sequence of randomly generated numbers every single time, we have to set the seed prior to simulating.

set.seed(1)
rnorm(5)
## [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078
set.seed(1)
rnorm(5)
## [1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078

Simulating from Linear Models

Linear model with Gaussian errors

Simulating from a simple linear model is fairly straightforward and requires only a few lines of code. These models have both a deterministic component, and a stochastic component. The minimal requirements for simulating the deterministic part of this type of model are defining the intercept, \(\beta_0\), and slope, \(\beta_1\), and to set up the \(x\) values you are interested in. These pieces can then be used to calculate the deterministic part of the model using the standard equation for a linear model \(y = \beta_0 + \beta_1 \times x\).

B_0 <- 2
B_1 <- 1
x <- 1:20
y_det <- B_0 + B_1 * x
y_det
##  [1]  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22

With the deterministic part specified, the next step is to add the stochastic component to the model. Here what we want is 20 random, normally distributed values, each with a mean equal to the deterministic component. This can be achieved by combining the deterministic predictions with the rnorm() function

y <- rnorm(n = 20, mean = y_det, sd = 2)
y
##  [1]  1.359063  4.974858  6.476649  7.151563  6.389223 11.023562  9.779686
##  [8]  8.757519  6.570600 14.249862 12.910133 13.967619 16.887672 17.642442
## [15] 18.187803 19.837955 20.564273 20.149130 17.021297 23.239651

Note: This same result could be achieved by adding mean 0 error to each deterministic prediction because errors are additive for this model \(y_i = \beta_0 + \beta_1 \times x_i + \varepsilon_i, \quad \varepsilon_i \sim \mathcal{N}(0, \sigma^2)\).

y <- B_0 + B_1 * x + rnorm(n = 20, mean = 0, sd = 2)
y 
##  [1]  2.887743  3.688409  2.058495  5.043700  7.835883 10.717359  8.794425
##  [8] 10.775343 10.892390  9.245881 12.170011 13.211420 14.881373 18.200051
## [15] 18.526351 17.670953 18.493277 21.393927 22.113326 20.622489

The problem with building a simulation this way, however, is that errors are only additive for the normal distribution, so this does not work for stochasticity that is drawn from other distributions.

If you intend on carrying out anything more than a simple simulation, it is usually more efficient to package everything together into a custom function.

Linear <- function(x){
  B_0 <- 2
  B_1 <- 1
  sigma <- 2
  y_det <- B_0 + B_1 * x
  y <- B_0 + B_1 * x + rnorm(n = length(x),
                             mean = y_det,
                             sd = sigma)
  y 
}

Linear(1)
## [1] 4.58501
Linear(1:5)
## [1]  6.729164  9.537066  9.775308 13.762215 14.796212

Simulating Nested Data

We often work with nested data, where there can be some normally distributed differences between groups (species, treatments, study sites, etc.). To simulate nested data with random slopes or intercepts, we need to first define the population level parameters, and then draw the individual variation around the population level trends from a mean 0 normal distribution. In essence, this requires adjusting the population level parameters by some normally distributed amount for each group.

Random Intercepts

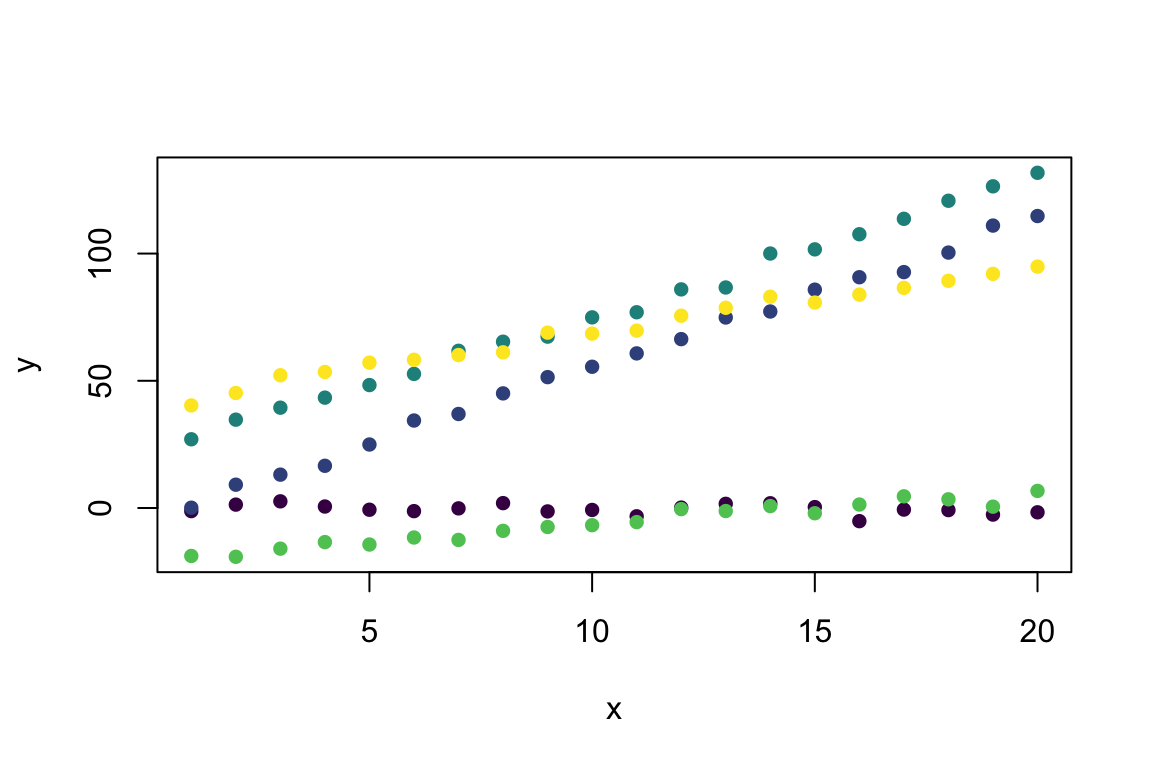
library(viridis)
#5 groups each with 4 data points
group <- factor(rep(1:5, each = 20))                              # 5 groups sampled 20 times
x <- rep(1:20, 5)                                                 # Define x values

Mixed_Linear <- function(x, group) {
  B_0 <- 2                                                        # Pop. level intercept
  B_1 <- 1                                                        # Pop. level slope
  Rand_Int <- rnorm(n = unique(group), sd = 10)                   # Random Intercepts
  y_det = (B_0 + Rand_Int[group]) + B_1*x                         # Deterministic prediction
  rnorm(n = length(x), mean = y_det, sd = 2)                      # Add stochasticity
}

y <- Mixed_Linear(x, group)                                       # Predict from the model

plot(y ~ x, col = viridis(5)[group], pch = 16)                    # Visualise with viridis colours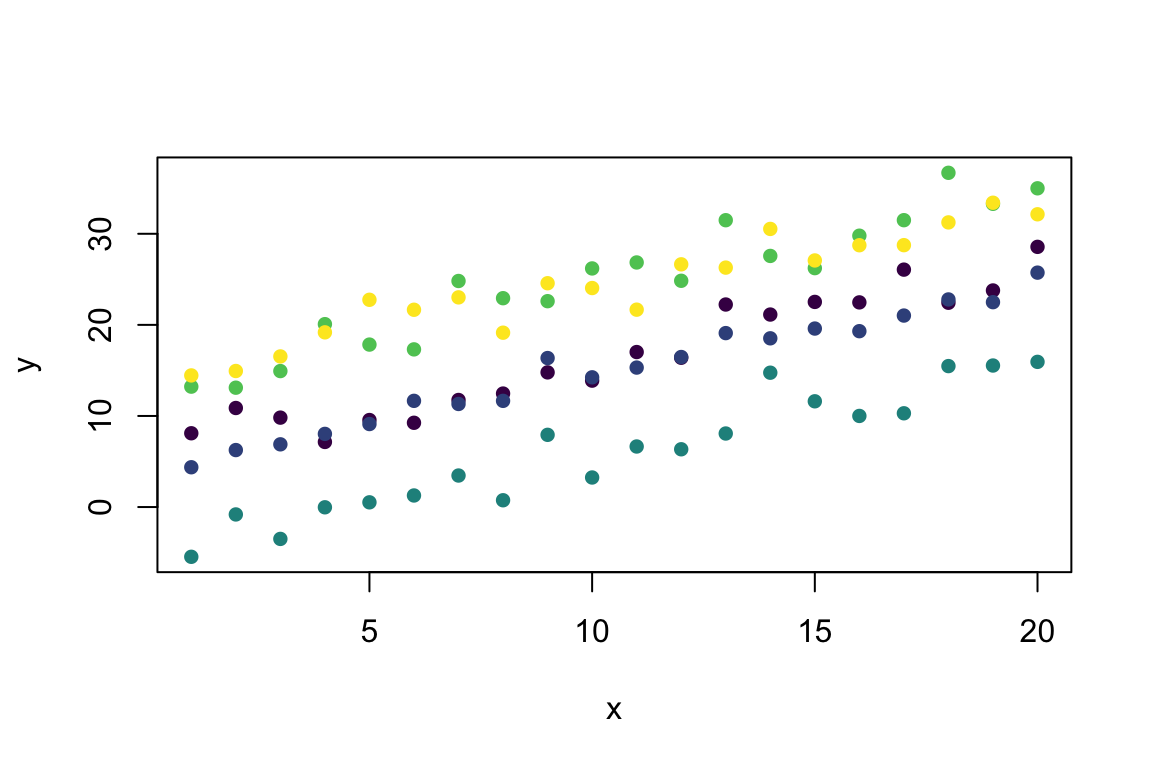

Random Slopes

group <- factor(rep(1:5, each = 20))                              # 5 groups sampled 20 times
x <- rep(1:20, 5)                                                 # Define x values

Mixed_Linear <- function(x, group) {
  B_0 <- 2                                                        # Pop. level intercept
  B_1 <- 1                                                        # Pop. level slope
  Rand_Slope <- rnorm(n = unique(group))                          # Random Slopes
  y_det = B_0 + (B_1+ Rand_Slope[group])*x                        # Deterministic prediction
  rnorm(n = length(x), mean = y_det, sd = 2)                      # Add stochasticity
}

y <- Mixed_Linear(x, group)                                       # Predict from the model

plot(y ~ x, col = viridis(5)[group], pch = 16)                    # Visualise with viridis colours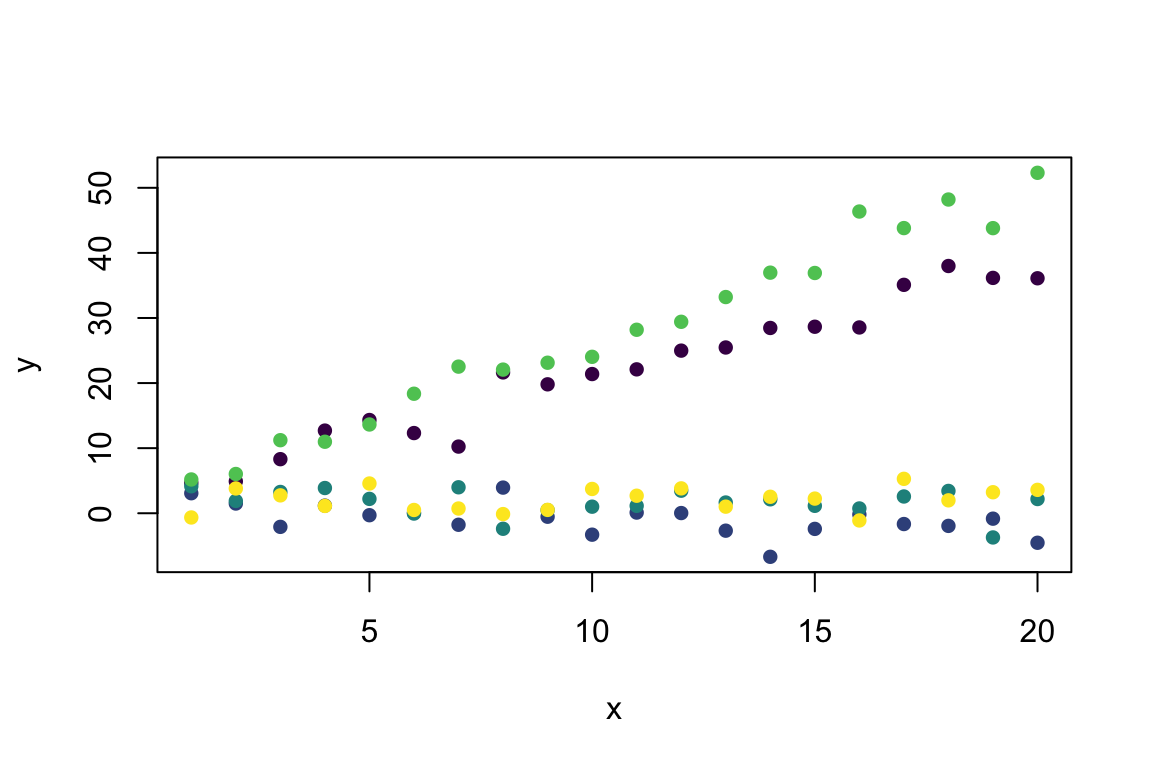

Random Slopes and Intercepts

group <- factor(rep(1:5, each = 20))                              # 5 groups sampled 20 times
x <- rep(1:20, 5)                                                 # Define x values

Mixed_Linear <- function(x, group) {
  B_0 <- 2                                                        # Pop. level intercept
  B_1 <- 1                                                        # Pop. level slope
  Rand_Int <- rnorm(n = unique(group), sd = 20)                   # Random Intercepts
  Rand_Slope <- rnorm(n = unique(group), sd = 3)                  # Random Slopes
  y_det = (B_0 + Rand_Int[group]) + (B_1+ Rand_Slope[group])*x    # Deterministic prediction
  rnorm(n = length(x), mean = y_det, sd = 2)                      # Add stochasticity
}

y <- Mixed_Linear(x, group)                                       # Predict from the model

plot(y ~ x, col = viridis(5)[group], pch = 16)                    # Visualise with viridis colours

Simulating Temporally Autocorrelated data

Simulating temporally correlated errors requires first defining an autocorrelation structure to simulate from, building the appropriate correlation matrix, and then using that to generate autocorrelated errors.

library(nlme)

n <- 500              # Sample size
B_0 <- 2              # Intercept
B_1 <- 1              # Slope
x <- runif(n, 1, 10)  # Values of the x variable
time <- 1:n           # Values of the time covariate
sigma <- 10           # Population level standard deviation
rho <- 0.80           # Temporal autocorrelation

# define a constructor for a first-order correlation structure
ar1 <- corAR1(form = ~ time, value = rho)
# initialize this against our data
AR1 <- Initialize(ar1, data = data.frame(time))
# generate the correlation matrix
V <- corMatrix(AR1)
# Cholesky factorization of V
Cv <- chol(V)
# simulate AR1 errors
e <- t(Cv) %*% rnorm(n, 0, sigma)  # cov(e) = V * sig^2
## generate response with AR1 errors
y <- B_0 + B_1 * x + e